RDieHarder 0.1.2
RDieHarder is an R package providing access to the DieHarder battery of tests for random number generators developed by Robert G. Brown and others. DieHarder had been updated to version 3.1.1 a while back, and I had been a little behind with updating RDieHarder. Version 0.1.2 rectifies this.The package still comes with a vignette describing both DieHarder and the RDieHarder package. And because pictures speak louder than a thousand (blogged) words, here is the first chart from the vignette:
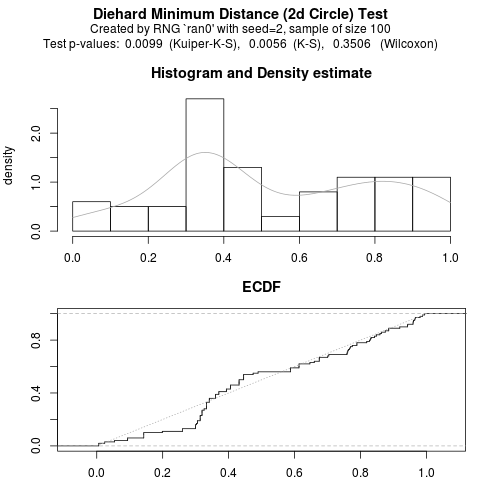

ran0 function. The histogram illustrating the distribution of
test scores is somewhat uneven. An ideal (and asymptotic) outcode is a
uniform distribution of p-values from the test. The empirical cumulative
distribution function (ECDF) below indicates a somewhat pronounced departure from
the diagonal. Informally speaking, this is what the
(Kuiper-)Kolmogorov-Smirnov test quantifies, and we see (in the text in the
chart) that the null of can be rejected an conventional levels. Based on
this example (which had a short run-time with few samples) we would indeed mistrust
this (known bad) RNG.
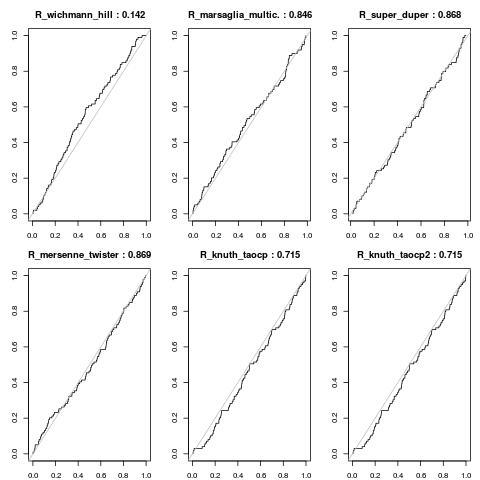
On the right, we have a more recent and trusted RNG, the well-known Mersenne Twister. The ten histogram buckets are all closer to the expected value of one-tenth, the estimated density is closer to flat, the ECDF is closer to the diagonal and the tests don't reject---so no reason to mistrust this RNG based on this test alone.
RDieHarder lets you run a battery of such tests against a boatload of known RNGs. Here is a second example, comparing the six RNGs built into R itself:
Courtesy of CRANberries, there is also a diffstat report for 0.1.2 relative to the older 0.1.1 release. More detailed information is on the RDieHarder page.