Overview
The file randmt.cc provides three new commands for GNU Octave:randmt to generate U(0,1) random numbers, randmtn to generate N(0,1) random numbers, and randmtseed to set the seed of the generator.
The actual ANSI C implementation of the RNG is provided by the file cokus.c (also included in the tarball), written by Shawn Cokus. This is an improved implementation of the very long period, fast, and memory-efficient Mersenne Twister Random Number Generator by Makoto Matsumoto and Takuji Nishimura. This random number generator uses a twisted generalized feedback shift-register algorithm which has a Mersenne prime period of 2^19937 - 1, or about 10^6000, and is equi-distributed in 623 dimensions. It has passed the `DIEHARD' statistical tests by Marsaglia, but is also extremely fast and efficient in terms of memory usage. The code has been tested on 32bit (i386) and 64bit (alpha) versions of Linux.
Beyond the actual MT implementation by Shawn Cokus, one routine from the RANDLIB library (Brown, Lovato, Russell, Venier, 1997, available at MDACC) was used to tranform uniform into standard normal deviates. This is the Ahrens and Dieter (1973) algorithm. I have simply combined the pieces, and provided simple C++ wrappers so that Octave can access this code. Also included are a Makefile, and a simple Octave script to time the MT RNG against Octave's default RNG from RANDLIB.
Provided mkoctfile is in your PATH, you can just type make to build the Octave modules randmt.oct, randmtn.oct, and randmtseed.oct. The `compare_rngs.m' Octave script can be used to time this RNG against the default RNG.
This package is released under the GNU GPL just like Octave, the MT and RANDLIB.
Speed comparison
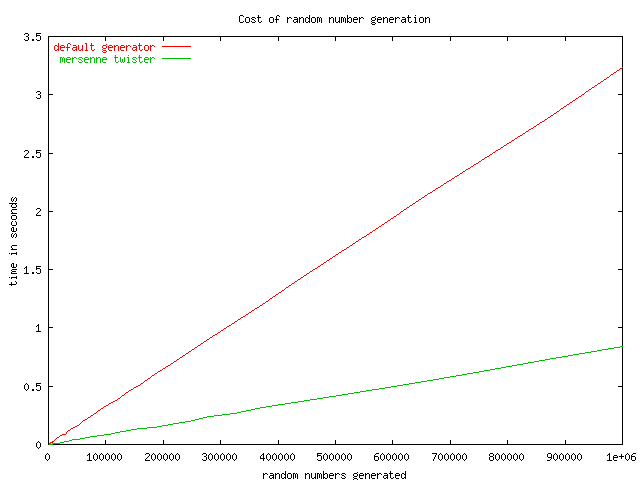
To give a rough idea of the speed improvement, consider the following
simple program which times
Octave's standard RNG, and the Mersenne Twister.
Reference
This RNG is fully documented at the Mersenne Twister RNG page, and the following paper provides the technical details:
@Article{Matsumoto_Nishimura98,
author = {Makoto Matsumoto and Takuji Nishimura},
title = {Mersenne Twister: A 623-dimensionally
equidistributed uniform
pseudorandom number generator},
journal = {ACM Transactions on Modeling and
Computer Simulation},
year = 1998,
volume = 8,
number = 1,
pages = {3-30},
note = {Code and information available at
\url{http://www.math.keio.ac.jp/matumoto/emt.html}}
}