Overview
RQuantLib connects GNU R with QuantLib.
What is R ?
GNU R, to quote from its highly recommended website, is `GNU S’ - A language and environment for statistical computing and graphics. R is similar to the award-winning S system, which was developed at Bell Laboratories by John Chambers et al. It provides a wide variety of statistical and graphical techniques (linear and nonlinear modelling, statistical tests, time series analysis, classification, clustering, …).
R is designed as a true computer language with control-flow constructions for iteration and alternation, and it allows users to add additional functionality by defining new functions. For computationally intensive tasks, C, C++ and Fortran code can be linked and called at run time. R is an official part for the GNU R.
What is QuantLib ?
QuantLib, to quote in turn from its website, is aiming to provide a comprehensive software framework for quantitative finance. QuantLib is a free/open source library for modeling, trading, and risk management in real-life. QuantLib is written in C++ with a clean object model, and is then exported to different languages such as Python, Ruby, Guile, MzScheme, Java, Perl, … via SWIG. .
So what can RQuantLib (currently) do?
There are two core areas of pricing: options, and fixed income. Utilities such as calendaring functions are also available.
Option Pricing
RQuantLib started with support for (vanilla and exotic) equity options. Standard European and American exercises are supported as well as Binary and Barrier options. Asian options are supported with both geometric and arithmetic compounding.
For all of the option types, upon evaluation an element of a simple class is returned. Each of the the specific option classes inherits from a base class Option, and print and summary methods are provided for the base class.
Moreover, another base class ImpliedVolatility is provided with methods print and summary and implied volatility solvers for European and American are provided (Binaries seem to trigger a QuantLib bug as far as I can tell).
For both option and implied volatility calculations, operations are limited to the scalar case. However, using the R, or rather, S object framework makes the work fairly convenient.
Lastly, for the basic European Option, an “array” interface is provided. Here, any of the usual input variables is allow to be in vector form. Solutions are then computed for the “multi-dimensional outer product” of all input vectors. Concretely, if called with three strike prices, four maturities and five volatilities, then 3 * 4 * 5 arrays are returned for the common variables of interest (i.e. value, delta, gamma, …). In other words, value is now an array over all possible combination of all possible input values. This allows for very compact comparison and scenario analysis.
Fixed Income
Support for Fixed Income started in the 0.2.* releases. The DiscountCurve function constructs the spot term structure of interest rates based on input market data including the settlement date, deposit rates, futures prices, FRA rates, or swap rates, in various combinations. It returns the corresponding discount factors, zero rates, and forward rates for a vector of times that is specified as input.
The BermudanSwaption function prices a Bermudan swaption with specified strike and maturity (in years), after calibrating the selected short-rate model to an input swaption volatility matrix. Swaption maturities are in years down the rows, and swap tenors are in years along the columns, in the usual fashion. It is assumed that the Bermudan swaption is exercisable on each reset date of the underlying swaps.
Starting with release 0.3.0, a large number of additional Fixed Income functions have become available thanks to the work of Khanh Nguyen that was part of the the Google Summer of Code 2009 program. The new functions include support for (where we list the available help pages):
- CallableBond
- ConvertibleFixedCouponBond
- ConvertibleFloatingCouponBond
- ConvertibleZeroCouponBond
- Enum
- FittedBondCurve
- FixedRateBond
- FixedRateBondCurve
- FixedRateBondPriceByYield
- FixedRateBondYield
- FloatingRateBond
- ZeroCouponBond
- ZeroPriceByYield
- ZeroYield
The Fixed Income functions are a good illustration of the R/C++ interface provided by Rcpp.
Utilities
As a first example of available calendaring functions,
businessDay can compute whether a given date (scalar or
vector) is a business in a given ‘calendar’ which can be chosen from a
wide set of country and settlements choices.
What else is there?
There are lots more financial instruments covered in QuantLib. RQuantLib should grow to accomodate these. Help in writing the R wrappers would accelerate the provision of RQuantLib hooks for these.
The RQuantLib package also contains an animated OpenGL demo. Unfortunately, GL support is not always very stable for a variety of graphics cards and drivers on both Linux and Windows, so this may in fact crash instead of run. This really appears to a hardware or driver issue as the code runs fine on some hardware combinations.
As a simpler alternative, consider these animated graphs made from combing the Rgl snapshots which approximates the effect of the OpenGL animation.
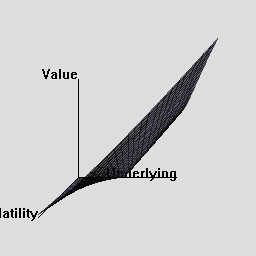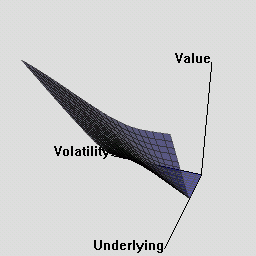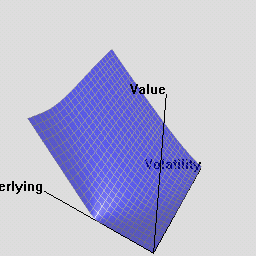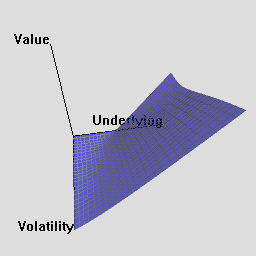
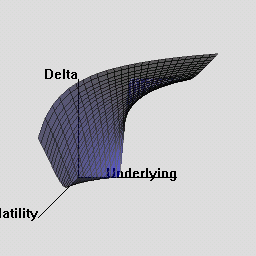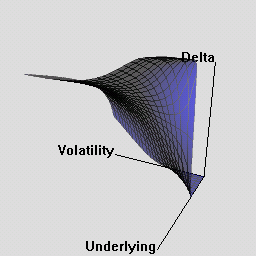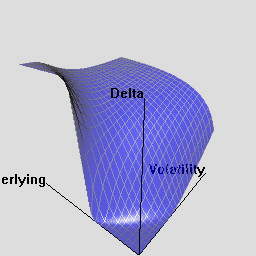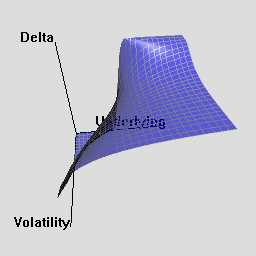
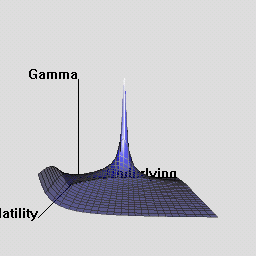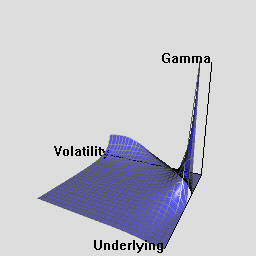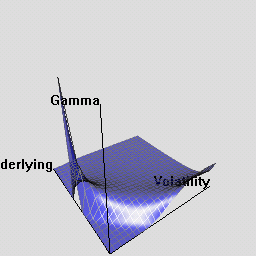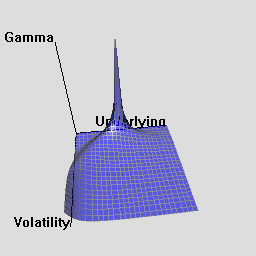

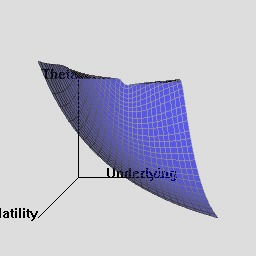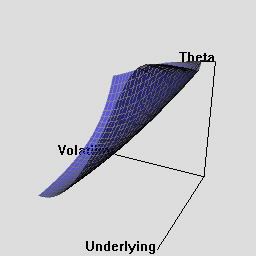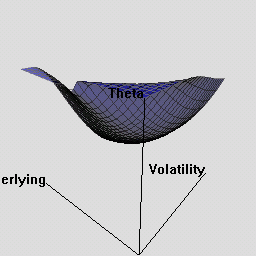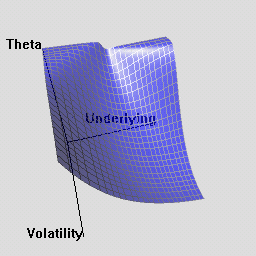
Examples
A simple example for EuropeanOption
Let’s start with a simple vanilla option, and look at the print and summary methods.
> library(RQuantLib)
> EO <- EuropeanOption("call", 100, 100, 0.01, 0.03, 0.5, 0.4)
> print(EO)
Concise summary of valuation for EuropeanOption
value delta gamma vega theta rho divRho
11.6365 0.5673 0.0138 27.6336 -11.8390 22.5475 -28.3657
> summary(EO)
Detailed summary of valuation for EuropeanOption
value delta gamma vega theta rho divRho
11.6365 0.5673 0.0138 27.6336 -11.8390 22.5475 -28.3657
with parameters
type underlying strike dividendYield riskFreeRate
"call" "100" "100" "0.01" "0.03"
maturity volatility
"0.5" "0.4"A simple example for EuropeanOptionImpliedVolatility
Let us now compute implied volatility for the same the option parameters as above, but at a price increased by 0.50. Note how we use the value element of the previous answer.
> EOImpVol <- EuropeanOptionImpliedVolatility("call", value=EO$value+0.50, 100, 100, 0.01, 0.03, 0.5, 0.4)
> print(EOImpVol)
Implied Volatility for EuropeanOptionImpliedVolatility is 0.418
> EOImpVol$impliedVol
[1] 0.4181017This shows also how the result value get be accessed directly.
An example of the array-style access
Here is an example of computing option values and analytics for several ranges of input values. For simplicit, we simply show the call to the built-in example from the RQuantLib documentation for this function:
> example(EuropeanOptionArrays)
ErpnOA> und.seq <- seq(10, 180, by = 5)
ErpnOA> vol.seq <- seq(0.2, 0.8, by = 0.1)
ErpnOA> EOarr <- EuropeanOptionArrays("call", underlying = und.seq,
strike = 100, dividendYield = 0.01, riskFreeRate = 0.03,
maturity = 1, volatility = vol.seq)
ErpnOA> old.par <- par(no.readonly = TRUE)
ErpnOA> par(mfrow = c(2, 2), oma = c(5, 0, 0, 0), mar = c(2,
2, 2, 1))
ErpnOA> plot(EOarr$parameter$underlying, EOarr$value[, 1],
type = "n", main = "option value", xlab = "", ylab = "")
ErpnOA> for (i in 1:length(vol.seq)) lines(EOarr$parameter$underlying,
EOarr$value[, i], col = i)
ErpnOA> plot(EOarr$parameter$underlying, EOarr$delta[, 1],
type = "n", main = "option delta", xlab = "", ylab = "")
ErpnOA> for (i in 1:length(vol.seq)) lines(EOarr$parameter$underlying,
EOarr$delta[, i], col = i)
ErpnOA> plot(EOarr$parameter$underlying, EOarr$gamma[, 1],
type = "n", main = "option gamma", xlab = "", ylab = "")
ErpnOA> for (i in 1:length(vol.seq)) lines(EOarr$parameter$underlying,
EOarr$gamma[, i], col = i)
ErpnOA> plot(EOarr$parameter$underlying, EOarr$vega[, 1],
type = "n", main = "option vega", xlab = "", ylab = "")
ErpnOA> for (i in 1:length(vol.seq)) lines(EOarr$parameter$underlying,
EOarr$vega[, i], col = i)
ErpnOA> mtext(text = paste("Strike is 100, maturity 1 year, riskless rate 0.03",
"\nUnderlying price from", und.seq[1], "to", und.seq[length(und.seq)],
"\nVolatility from", vol.seq[1], "to", vol.seq[length(vol.seq)]),
side = 1, font = 1, oute .... [TRUNCATED]
ErpnOA> par(old.par)The resulting chart looks as follows:
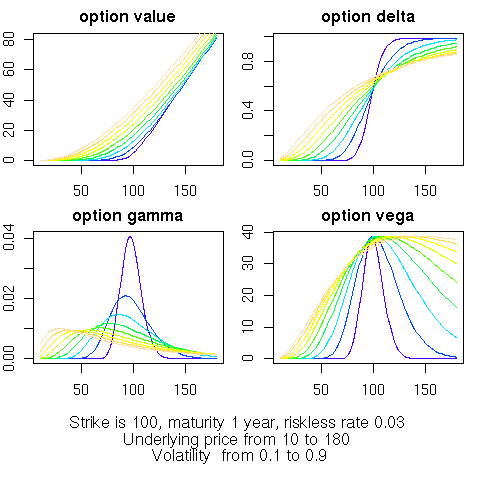
An example for DiscountCurves
The example in the DiscountCurve manual page follows:
> example(DiscountCurve)
DscntC> savepar <- par(mfrow = c(3, 3))
DscntC> params <- list(tradeDate = c(2, 15, 2002), settleDate = c(2,
19, 2002), dt = 0.25, interpWhat = "discount", interpHow = "loglinear")
DscntC> tsQuotes <- list(d1w = 0.0382, d1m = 0.0372, fut1 = 96.2875,
fut2 = 96.7875, fut3 = 96.9875, fut4 = 96.6875, fut5 = 96.4875,
fut6 = 96.3875, fut7 = 96.2875, fut8 = 96.0875, s3y = 0.0398,
s5y = 0.0443, s10y = 0.05165, s15y = 0.055175)
DscntC> times <- seq(0, 10, 0.1)
DscntC> curves <- DiscountCurve(params, tsQuotes, times)
DscntC> plot(curves, setpar = FALSE)
DscntC> params$interpHow = "linear"
DscntC> curves <- DiscountCurve(params, tsQuotes, times)
DscntC> plot(curves, setpar = FALSE)
DscntC> params$interpHow = "spline"
DscntC> curves <- DiscountCurve(params, tsQuotes, times)
DscntC> plot(curves, setpar = FALSE)
DscntC> par(savepar)The resulting chart looks as follows:
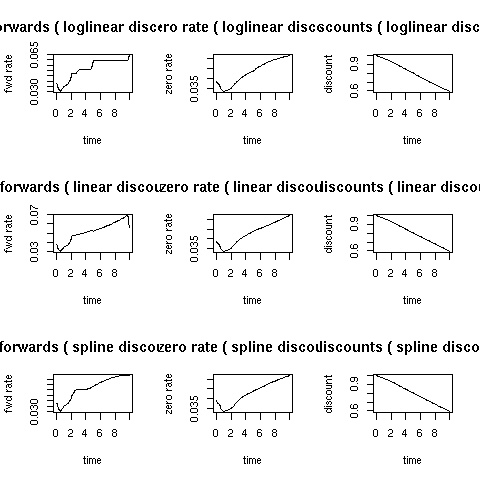
Download
From this machine, you can get the RQuantLib tar archive, the (old) reference manual or simply peruse the entire directory.
Alternatively, you can also get RQuantLib from a Comprehensive R Archive Network (CRAN)
Lastly, RQuantLib sources, after having been on r-forge, are now hosted at GitHub; please see the RQuantLib page for another short overview and access to the git archive. Issue tickets and pull request (ideally after initial discussion) are welcome.
Installation on Unix
It goes almost without saying that QuantLib must be installed in order to use RQuantLib as the latter package has to link against the libraries provided by the former libraries. If you do not have QuantLib, you will have to install it first prefore proceeding. The same now goes for the Boost C++ libraries.
For Debian users (as well as for
Ubuntu and other derivatives, this is as simple as saying
apt-get install libquantlib0 libquantlib-dev. Others will
have to compile QuantLib, see the QuantLib site.
Generally, for Linux or Unix users, the usual
R CMD INSTALL RQuantLib.tar.gz should work from outside R,
as should a call to install.packages(). At least, it does
on my Debian Linux system.
Feedback and comments are of course welcome in general, and in particular on the installation.
Installation on Windows
Thanks to the rwinlib repository for QuantLib which provides a static Windows library, Windows binary packages for R can be built so that CRAN can provide binaries as usual. Check the status of that repository for the QuantLib version used which may be behind, and consider contributing a current build.
Copyright
Copyright(c) 2002 - 2018 by Dirk Eddelbuettel
Copyright(c) 2015 - 2018 by Dirk Eddelbuettel and Terri Leitch
Copyright(c) 2009 - 2010 by Dirk Eddelbuettel and Khanh Nguyen
Copyright(c) 2005 - 2007 by Dominick Samperi
License
GPL (>= 2)


